Quiz Summary
0 of 30 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Results
0 of 30 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Current
- Review / Skip
- Answered
- Correct
- Incorrect
-
Question 1 of 30
1. Question
You have collected your portfolio’s daily profit and loss (P&L) for the most recent 100 traded days. You sorted (ranked) the outcomes from worst to best. Below are the ten worst days; e.g., the worst daily loss was -11.0.
You want to estimate the portfolio’s value at risk (VaR) under the historical simulation approach, and its expected shortfall. Which are, respectively, the portfolio’s 95.0% value at risk (VaR) and 95.0% expected shortfall (ES)?
CorrectIncorrect -
Question 2 of 30
2. Question
A $100.0 million equity portfolio contains two equally-weighted and uncorrelated (i.e., correlation equals zero) positions. The positions’ volatilities are 30.0% and 40.0% per annum. If their returns are i.i.d. normal, which is nearest to the 10-day 95.0% value at risk (VaR) if we assume 250 trading days per year?
CorrectIncorrect -
Question 3 of 30
3. Question
The following table shows the sorted worst six (6) returns, sorted, among a trailing window of 100 returns. For example, the worst return was -13.00% and it happened 14 days prior. The weights under simple historical simulation (HS) are compared to the weights under exponentially weighted moving average (EWMA) where lambda parameter is set equal to 0.920. For example, 20 days prior the return was -11.00% and this return is assigned a weight of (1-0.920)*0.920^(20-1)/(1-0.920)^100 = 1.64%.
If we assume that “1/2 of a given return’s weight is to the right and 1/2 to the left of the actual observation” and “the required VaR level is a linearly interpolated return, where the distance to the two adjacent cumulative weights determines the return,” which is nearest to the 95.0% value at risk (VaR) under the hybrid approach?
CorrectIncorrect -
Question 4 of 30
4. Question
You purchase an at-the-money (ATM) call option with a maturity of one year and a strike price of $60.00 while the non-dividend-paying stock price is also $60.00. The volatility of the stock is 50.0% and the risk-free rate is 4.0%. . There are 250 trading days in the year. If stock returns are i.i.d. normal and the stock’s daily expected return (drift) is assumed to be zero, which is nearest to the ten-day 95.0% delta-normal value at risk (VaR) of the long call option position? (please feel free to use this Z lookup table https://www.bionicturtle.com/images/2014/dailypq/P1.T4.410_1_zlookup.png)
CorrectIncorrect -
Question 5 of 30
5. Question
You have a long position in a call option with a one year maturity and strike price of $66.00 while the stock price is $70.00. The non-dividend-paying stock’s volatility is 50.0% per annum. The percentage (per option) delta is 0.6730 and its gamma is 0.010. The risk-free rate is 4.0%, the stock returns are i.i.d. normal, and we assume the daily stock drift is zero; alternatively, we are computing a relative VaR. There are 250 trading days in the year. If we include the gamma term (aka, quadratic VaR), which is nearest to the 10-day 99.0% confident value at risk (VaR) of the long position in the option?
CorrectIncorrect -
Question 6 of 30
6. Question
The price of $1,000 face value 20-year zero-coupon bond is $135.34 due to a yield of 10.0% per annum. The daily yield volatility is 1.0% with normally distributed yields. All yields are expressed with continuous compounding. Which is nearest to the 95.0% confident daily (quadratic) value-at-risk; quadratic VaR incorporates both duration and convexity?
CorrectIncorrect -
Question 7 of 30
7. Question
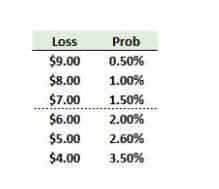
Your colleague has defined a discrete loss distribution. The tail of the loss distribution is shown below; for example, the worst loss of $9.00 will happen with a probability of 0.50%, a loss of $8.00 will occur with a probability of 1.00%.
The entire distribution spans 25 outcomes ranging from a $9.00 loss to a $15.00 gain, although only the six worst losses are shown. Which is nearest to the 95.0% expected shortfall (ES)?
CorrectIncorrect -
Question 8 of 30
8. Question
Which of the following is necessarily true of expected shortfall (ES)?
CorrectIncorrect -
Question 9 of 30
9. Question
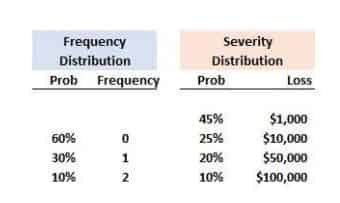
On any given day, a frequency distribution indicates that the probability of a single loss event is 30% and the probability that two loss events occur is 10% such that on 60% of days there will be no loss events. For each loss event that does occur, there are four possible severity outcomes: a loss of $100,000 with 10% probability, a loss of $50,000 with 20% probability, a loss of $10,000 with 25% probability, and a loss of $1,000 with probability of 45%. As shown below:
Which is nearest to the 99.0% expected shortfall (ES) of the aggregate (tabulated) loss?
CorrectIncorrect -
Question 10 of 30
10. Question
A deeply out-of-the-money European call option with a one-year maturity has a strike price of $35.00 while the asset price is $20.00. The non-dividend-paying asset has a volatility of 40.0% per annum while the risk-free rate is 8.0% per annum with continuous compounding. You want to value the option with a four-step binomial (each step is three months) and, per the Cox, Ross, Rubinstein model, the magnitude of each up jump (u) is given by (u) = exp[σ*sqrt(Δt)]. You realize that although there are 16 different possible paths to maturity, due to the high strike price only one path (i.e., four consecutive up jumps) produces a path where the option has intrinsic value at maturity. Recall that a = exp[r*Δt] and p = (a-d)/(u-d). Which is nearest to the value of this option?
CorrectIncorrect -
Question 11 of 30
11. Question
Consider a binomial tree with 12 steps where each time step is one month such that an option matures in one year. The underlying asset volatility is 28.0% per annum which implies the magnitude of an up jump is approximately 8.42%; i.e., u = exp[σ*sqrt(Δt)] = exp[0.28*sqrt(1/12)] = 1.0842. If the riskless rate is 4.0%, the probability of an up jump (p) is about 50%; i.e., p = [exp(0.04*1/12) – exp[-0.28*sqrt(1/12)]/(u – d) = 0.5004, which we will round to 0.50. Which is nearest to the probability that the asset price finishes the year, at T = 1.0 on the binomial tree, at the same price it started the year?
CorrectIncorrect -
Question 12 of 30
12. Question
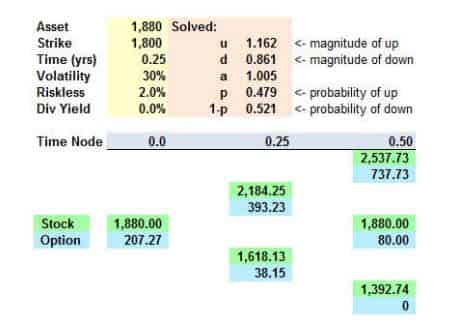
The snapshot below displays the value of six-month European call option on the S&P 500 Index, as prepared by your colleague Peter. The call option is in-the-money (ITM) as the strike price is 1800 while the Index price is 1880. According to this two-step binomial tree, the price of the option is $207.27.
However, you realize the dividend yield should be 2.0%. What is the impact of changing the dividend yield input from zero to 2.0%?
CorrectIncorrect -
Question 13 of 30
13. Question
A six-month (T = 0.5 years) European call option has a strike price of $50.00 while the asset price is $55.00. The asset’s volatility is 34.0% per annum and it does not pay a dividend. The risk-free rate is 4.0%. If we assume that N(d1) = N(0.600) = 0.7257 and N(d2) = N(0.359) = 0.6404, which is nearest to the price of the call?
CorrectIncorrect -
Question 14 of 30
14. Question
A six-month (T = 0.5 years) at-the-money European put option has a strike price equal to the current stock price of $20.00 while the riskless rate is 4.0% and the stock pays no dividends. The volatility of the underlying asset price is 34.0% per annum. If we assume that N(d1) = N(0.2304) = 0.5806 and N(d2) = N(-0.0370) = 0.4852, which is nearest to the price of the put?
CorrectIncorrect -
Question 15 of 30
15. Question
An out-of-the-money (OTM) European call option with a maturity of one year (T = 1.0 year) has a strike price of $40.00 while the current price of the non-dividend-paying asset is $30.00. The volatility of the underlying asset price is 44.0% per annum and the risk-free rate is 2.0%. The price of the call is $2.48 because per the Black-Scholes option pricing model (BSM OPM) $2.48 = $30*0.3489 – $40*exp(-0.020*1.0)*0.2037. Each of the following is true about this call option EXCEPT which is false?
CorrectIncorrect -
Question 16 of 30
16. Question
Trader Jane writes 100 call options with a five year maturity and strike price of $35.00 on a stock that pays a 6.0% dividend (T = 5.0, q = 6.0%). Each call option has a percentage delta of exactly 0.500. If she wants to use put options with the same strike price and maturity, which trade will approximately neutralize the net position delta?
CorrectIncorrect -
Question 17 of 30
17. Question
Trader Bob holds a delta-neutral portfolio but his position gamma is +600. Using call options with percentage delta of 0.50 and percentage gamma of 0.30, which trades neutralize both delta and gamma simultaneously?
CorrectIncorrect -
Question 18 of 30
18. Question
A long position in European call options is approaching its expiration such that its maturity is near zero. The options happen to be nearly at-the-money; i.e., the current asset price is nearly equal to the strike price. Which of the following is most likely true?
CorrectIncorrect -
Question 19 of 30
19. Question
The price of a six-month zero-coupon bond is $99.30. The price of a one-year 6.0% coupon bond is $101.98. The face value of both bonds is $100.00 and the rates are expressed per annum with semi-annual compounding; aka, bond-equivalent basis. Which is nearest to the implied one-year spot rate?
CorrectIncorrect -
Question 20 of 30
20. Question
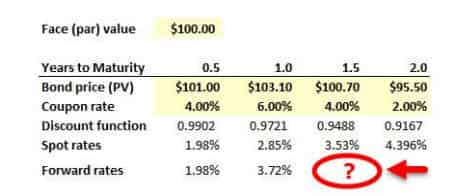
Below are listed four bonds at various maturities from six months to two years. Along with the price of each bond is listed its coupon rate, the discount factor for its maturity, and the spot rate at each maturity:
For example, the one-year spot rate, r(1.0), is about 2.85% based on a one-year discount factor, df(1.0), of 0.9271; and the six-month forward rate in six months, f(0.5,1.0), is equal to 3.72%. All rates are expressed per annum with semi-annual compounding. Which is nearest to the six month forward rate beginning in one-year, f(1.0, 1.5)?
CorrectIncorrect -
Question 21 of 30
21. Question
The price of a four-year zero-coupon government bond is $86.00. The price of a similar five-year bond is $79.51. If we assume all rates are expressed per annum with semi-annual compounding, which is nearest to the one-year implied forward rate from year four to year five; i.e., f(0.4, 0.5)?
CorrectIncorrect -
Question 22 of 30
22. Question
A bond with a 1.5 year maturity has a coupon rate of 12.0% and pays the coupon semi-annually. The spot rate curve is very steep: 1.0% at 0.5 years, 2.0% at 1.0 years and 3.0% at 1.5 years. Because the spot rates are per annum with continuous compounding, the bond’s price is $6.00*exp(-0.01*0.5) + $6.00*exp(-0.02*1.0) + $106*exp(-0.03*1.5) = $113.19. Under a scenario assumption of realized forwards–i.e., “[realized forwards] is to assume that forward rates equal expectations of future rates and that, as time passes, these forward rates are realized” says Tuckman–which is nearest to the bond price in six months?
CorrectIncorrect -
Question 23 of 30
23. Question
A bond with a 1.5 year maturity has a coupon rate of 4.0% and the coupon pays semiannually. The forward rate curve is very steep and high: 2.0% at six months, 4.0% at 1.0 years and 7.0% at 1.5 years, all rates per annum with semi-annual compounding. The bond price is therefore $99.5833 with a yield (yield-to-maturity) of 4.290%. Under a scenario assumption of an unchanged term structure (in contrast to “realized forwards”), which is nearest to the
expected yield (YTM) of the bond six months in the future?CorrectIncorrect -
Question 24 of 30
24. Question
Consider a bond with a maturity of (T) years when the spot rate curve is upward-sloping. In six months, when the bond’s maturity is (T-0.5 years) which of the following is necessarily TRUE about the bond’s price?
CorrectIncorrect -
Question 25 of 30
25. Question
Consider a 1.5 year bond that pays a 9.0% semi-annual coupon. Under the following spot/forward rate curves, the bond’s price is $110.22, as follows:
As the rates are expressed with semi-annual compounding, which is nearest to the bond’s (modified) duration?
CorrectIncorrect -
Question 26 of 30
26. Question
A zero-coupon bond with a 20-year maturity has a face value of $1,000 when the yield curve is flat at a certain per annum rate with continuous compounding. If the yield increases by 80 basis points (0.80%), which is nearest to the estimated decrease in the bond price in percentage terms?
CorrectIncorrect -
Question 27 of 30
27. Question
Which is nearest to, respectively, the effective duration and effective convexity of a 15-year bond that pays a 9.0% semi-annual compound and yields 12.0% per annum with semiannual compounding?
CorrectIncorrect -
Question 28 of 30
28. Question
In regard to a borrower’s liability, the exposure amount (EA) is $1.0 million with a default probability of 10.0% and a loss given default (LGD; aka, loss rate) of 70.0%. The standard deviation of the loss rate, sigma(LGD), is 16.0%. Which are nearest, respectively, to the exposure’s expected loss (EL) and unexpected loss (UL)?
CorrectIncorrect -
Question 29 of 30
29. Question
A portfolio contains two credit assets with identical profiles. Each is a $1.0 million exposure amount (EA) with a default probability (PD) of 10.0% and loss given default (LGD) of 30.0%. The standard deviation of the LGD is 20.0%. The default correlation between the two credit assets is 20.0%. Which is nearest to the portfolio’s unexpected loss (portfolio UL)?
CorrectIncorrect -
Question 30 of 30
30. Question
A portfolio contains two credit assets with unexpected losses (UL), respectively, of $110,000 and $200,000. As their default correlation is 22.0%, the portfolio unexpected loss is $248,556. Which is nearest to the risk contribution (RC) of the asset with the greater risk contribution?
CorrectIncorrect