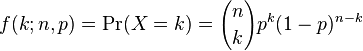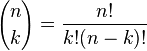Credit VaR

[Swarnendu Pathak]

Hi,
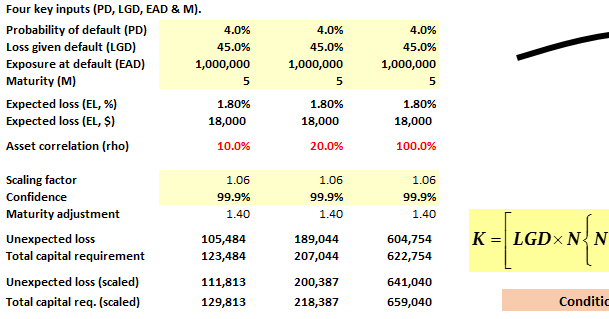
In the chapter Portfolio credit Risk (Allan M Malz) regarding the CVaR it is mentioned that when the PD is less then the significance level, then CVaR would be (-) ve or there would be a gain instead of loss as extreme loss is Zero, and if PD is more than significance level then CVaR is EAD*(1-Recovery Rate) minus LDG*PD (expected loss). Please explain when PD is less than significance level why extreme LGD is zero??

Thanks

 

[David Harper CFA FRM]

Hi Swarnendu,

I cannot locate your reference specifically (and i am unclear what you mean be "extreme LGD") however I think I know to what general concept you refer. Consider a single bond with face value of $100 and PD = 3% such that its expected loss (EL) is $3. The 95% VaR is zero due to distribution and the fact that the PD of 3% is less than the VaR significance of 5%; i.e., the 95% quantile is located at "no default!" (note we can argue this is a weakness of VaR via lack of subadditivity).

Now consider that Malz defines 95% Credit VaR = worst loss at 95% quantile - expected loss. By deducting expected loss, CVAR = UL and can be called a "relative VaR"

But we see the "problem:" 95% Credit VaR = 0 - $2 = -2, as the quantile is awkwardly less than the mean! I hope that helps,

 

[Success2014]

Hi, regarding this same topic. Table 7-1 (maz, chapter 8: portfolio credit risk) in the curriculum, shows n=1, and compares PD = 0.005, 0.02, and 0.05 on a 1bln portfolio. EL is 5mln, 20mln and 50mln respectively. Number of defaults is 0,1, and 1 respectively. 95% confidence interval. How do we calculate the number of defaults? The books shows 1 default, when PD is 2%, but shouldn't we expected 0 defaults since 95% confidence interval? THanks

 

[David Harper CFA FRM]

Hi @Success2014 Here is my XLS replication of Malz 8-1:
https://www.dropbox.com/s/adu1cec81illtkq/Malz_Fig 8.1_CVaR.xlsx?dl=0
i.e., number of defaults = BINOM.INV(n, pd, confidence)
note: his staked table of 3*6 corresponds to my 18 columns

You are correct that if n = 1 and PD is 2%, then number of defaults (quantile function) at 95% confidence is zero, simply because 2 % PD < 5% significance, but Malz Table 8.1 shows (for n =1) defaults = 0 at 95% confidence and defaults = 1 and 99% confidence, which is also correct as 2% pd > 1% sig.

Actually, the only difference between my XLS and Malz 8-1 is where he shows (for n = 1) 0 defaults when PD = 5% and confidence = 95%; but this is just a matter of interpretation of VaR in the case of a discrete distribution (I like Excel's conservative outcome). My notes omitted the n = 1 case, it's anyways unrealistic I think. I hope that helps, thanks,

 

[Success2014]

Can this calculation be done on a calculator? For instance, column J in the spreadsheet shows - n=50, p=2%, CI=95%...is this a calc we need to know for the exam? Seems as though, we get the problem and answer in reading, but no calcs. Thanks, S

 

[David Harper CFA FRM]

@Success2014

In a way, technically, it is a calculation you want (or need) to know:

• On the one hand, this CVaR exhibit (e.g., Column J) is overall too tedious to appear on the exam. As evidence, note the AIMs associated with this entire chapter are qualitative (GARP has no "calculate" or "compute" verbs for good reason). See below.
  
• On the other hand, the binomial as a component is highly testable. GARP loves this sort of question. For example, given n = 50, pd = 2.0% and confidence = 95.0% is a classic "FRM-type" question! Because you can retrieve it by computing only three binomials; eg., Prob ( x = 0 | n = 50, p=2%) = 0.98^50, and separate calcs for each binomial for Prob (x = 1), Prob (x = 2) and Prob (x = 3) shows the 95% confidence is 3 defaults (although, FWIW, actual exam would limit it to fewer PMF calcs but that doesn't change the need to understand what's going on here). It is true "we get the problem and answer in reading, but no calcs," but binomial is elsewhere in syllabus (and clearly under scope).

So, short answer (IMO), the AIMs are good here: don't worry beyond concept, but understand and be able to replicate the binomial component. Thanks,

Malz Chapter 8 AIMs:

• Define default correlation for credit portfolios.
• Identify drawbacks in using the correlation-based credit portfolio framework.
• Assess the impact of correlation on a credit portfolio and its Credit VaR.
• Describe the use of a single factor model to measure portfolio credit risk, including the impact of correlation.
• Describe how Credit VaR can be calculated using a simulation of joint defaults with a copula.

 

[Success2014]

Can this calculation be done on a calculator? For instance, column J in the spreadsheet shows - n=50, p=2%, CI=95%...is this a calc we need to know for the exam? Seems as though, we get the problem and answer in reading, but no calcs. Thanks, S

I found this formula, but doesn't work in all cases...assuming I'm applying correctly.

 

[David Harper CFA FRM]

@Success2014 That is the formula for the confidence interval of a sampled default rate with normal approximation, see http://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval
... but it's not applied in the CVaR exhibit above, as the above does not have any sampling. The binomial distributions are fully specified with (eg) n = 50 and pd = 5% and the exercise is retrieving a VaR (quantile) from the binomial distribution; e.g., column J uses Excel's =BINOM.INV(n, pd, confidence%) as a quantile function (ie., inverse cumulative distribution function).

 

[Success2014]

@Success2014 That is the formula for the confidence interval of a sampled default rate with normal approximation, see http://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval
... but it's not applied in the CVaR exhibit; e.g., column J uses Excel's =BINOM.INV(n, pd, confidence%) as a quantile function (ie., inverse cumulative distribution function).

Thanks for being patient with my question. I am forgetting the basics. You say binomial needs to be known for the exam, but we won't have excel on the exam. I was wondering how to calculate w/o excel on actual exam...

Excel is easy just need to know =BINOM.INV(n, pd, CI%)...

With: n=50, p=2%, CI=95%... does this formula look right? defaults = (50 x 49 x 48 / 3 x 2 x 1) x (.02^3) x (.98^47)?

I get .0606...

for k = 0, 1, 2, ..., n, where

 

[David Harper CFA FRM]

Hi @Success2014 yes, correct! You've solved for the Prob(X = 3) or Prob(3 defaults given n = 50 and PD = 2%). That's a PMF.
If you do that for each of X = 0, X = 1, X = 2, and X = 3, you get:

• Prob(x = 0 defaults) = 0.36416968
• Prob(x = 1 defaults) = 0.371601714
• Prob(x = 2 defaults) = 0.185800857
• Prob(x = 3 defaults) = 0.060669668

CVaR, as quantile, concerns the cumulative, so the 95% CVaR here is based on 95% confidence that the number of defaults will be three or less (a CDF not a PMF question). Here, we'd have to add them up, note that Pr(0) + Pr(1) + Pr(2) ~= 92.2% which implies that the 95% quantile lies "beyond" 2 defaults; another way to put this is, the 92.2% quantile (confidence) occurs at 2 defaults. When we add Pr(3) we get a cumulative of 98.2%, so bingo!, we've found where 95% lies.

B/c this is four calcs, this is 1 or 2 calcs more than an exam would ask. It takes too much time on an exam to do 4 binomial PMF calcs! But I have seen just this sort of question asked when 2 or 3 binomial PDFs calcs are needed. It's a good question: it tests an understanding of distributions. Thanks,

 

[Success2014]

Hi @Success2014 yes, correct! You've solved for the Prob(X = 3) or Prob(3 defaults given n = 50 and PD = 2%). That's a PMF.
If you do that for each of X = 0, X = 1, X = 2, and X = 3, you get:

• Prob(x = 0 defaults) = 0.36416968
• Prob(x = 1 defaults) = 0.371601714
• Prob(x = 2 defaults) = 0.185800857
• Prob(x = 3 defaults) = 0.060669668

CVaR, as quantile, concerns the cumulative, so the 95% CVaR here is based on 95% confidence that the number of defaults will be three or less (a CDF not a PMF question). Here, we'd have to add them up, note that Pr(0) + Pr(1) + Pr(2) ~= 92.2% which implies that the 95% quantile lies "beyond" 2 defaults; another way to put this is, the 92.2% quantile (confidence) occurs at 2 defaults. When we add Pr(3) we get a cumulative of 98.2%, so bingo!, we've found where 95% lies.

B/c this is four calcs, this is 1 or 2 calcs more than an exam would ask. It takes too much time on an exam to do 4 binomial PMF calcs! But I have seen just this sort of question asked when 2 or 3 binomial PDFs calcs are needed. It's a good question: it tests an understanding of distributions. Thanks,

Gotcha, two simple things were confusing me, not sure if others get caught up on this. I was originally thinking the number of defaults was as simple as alpha x sample...so 5% x 50 = 2.5 and rounds to 3, but I noticed as n got larger this calculation no longer worked. And this simple approach doesn't account for the probability of default. For instance, 5% x 1000 = 50, but number of defaults @ pd =2% = 28.

Last part - How do we determine the number of x's to calculate (x=0, x=1, x=2, x=3)? Is it as simple as keep calculating until the CDF adds to > 95% or 99% depending on our CVar confidence? For instance, we require to calculate a PMF for each x from 0 to 28 before the sum adds to greater than 95%...

Thanks so much, I am in a better spot conceptually.

 

[David Harper CFA FRM]

Hi @Success2014 sure thing!

Yes, that's exactly correct as far as I am concerned: Is it as simple as keep calculating until the CDF adds to > 95% or 99% depending on our CVar confidence?
... and that's why this particular example, which requires four (4) PMFs to be added until the confidence is reaches, would be about 2 calculations too long for the exam.

But the concept is that simple: adding the PMFs, by definition, is giving you the cumulative probability and the definition of VaR is: the (loss) value you find when you reach the confidence level on the cumulative distribution; aka, the quantile function, inverse CDF

Sometimes i think about simple examples to keep clear about it, like a six-sided die which has a simple PMF. Our binomial has more bins and they aren't uniform, but otherwise it's similar:

• pr(roll a 1) = 1/6 = 16.67% (PMF) and cumulative (CDF)= 16.7%
  
• pr(roll a 2) = 1/6 = 16.67% and cumulative = 33.3%
  
• pr(roll a 3) = 1/6 = 16.67% and cumulative = 50%
  
• pr(roll a 4) = 1/6 = 16.67% and cumulative = 66.7%
  
• pr(roll a 5) = 1/6 = 16.67% and cumulative = 83.3%
  
• pr(roll a 6) = 1/6 = 16.67% and cumulative = 100%

If 6 is the worst loss, what's the 95% VaR here? you basically add up the first five and get to 83.3% which is not far enough b/c it's less than 95% (we can only be 83.3% confident that we will roll a 5 or less). So we need to include the 6, which gets us "beyond" the confidence (100% vs 95%), so our 95% confidence falls within the PMF bin that holds 6 and that's the answer. True, b/c this is a dumb distribution, 6 happens to our 100% VaR and our 95% and our 85% VaR. But our 40% VaR here is 3. Maybe that helps, thanks!

 

[Linghan]

@David Harper CFA FRM Will Credit VaR affected by default correlation?

Thanks,

Ling

 

[QuantMan2318]

As the Worst Case Default Rate (WCDR), which is used in the computation of Credit VaR is affected by default correlation, I would hazard that the Credit VaR is affected by our estimates of the correlation.

https://courses.edx.org/c4x/DelftX/TW3421x/asset/Week6_PD3_2.pdf

This particular link shows the computation of Credit VaR, as the WCDR is based on an one factor copula model which does incorporate default correlations, we can assume that the Credit VaR is influenced by the same. FYI the WCDR is:


Which in turn has the coefficient of correlation based on the Basel rules as:



Hope this helps

Thanks

 

[Linghan]

As the Worst Case Default Rate (WCDR), which is used in the computation of Credit VaR is affected by default correlation, I would hazard that the Credit VaR is affected by our estimates of the correlation.

https://courses.edx.org/c4x/DelftX/TW3421x/asset/Week6_PD3_2.pdf

This particular link shows the computation of Credit VaR, as the WCDR is based on an one factor copula model which does incorporate default correlations, we can assume that the Credit VaR is influenced by the same. FYI the WCDR is:

View attachment 1146
Which in turn has the coefficient of correlation based on the Basel rules as:

View attachment 1147

Hope this helps

Thanks

THANKS!!!!

 

[David Harper CFA FRM]

awesome @QuantMan2318 ! @Linghan unexpected loss increases with default correction and therefore so does CVaR. Below is a display of the WCDR formula, same as QuantMan's above (implemented as the IRB function in Basel) where I quickly just show increasing correlation (in red) and its impact on UL and Total Capital (in Basel, CVaR = UL + EL, but the point is the correlation impacts unexpected loss). Here is the XLS https://www.dropbox.com/s/4vwkv9656cg5tib/0510-basel-irb.xlsx?dl=0

 

[QuantMan2318]

Thanks @David Harper CFA FRM ! Good to be back here and back in India again. I must say I loved the education offered in your country. The Excel is superb, I have downloaded it for my reference.

 

[ijooma]

Hi @David Harper CFA FRM
I have a question. In determining the CVar in Malz chapter 8, a binomial inverses function is used to derive the no of defaults table 8.1. For the exam are we required to calculate these as well. If so please can u provide some insights on how to go about this? Sorry this maybe a simple question.

 

[Nicole Seaman]

Hi @David Harper CFA FRM
I have a question. In determining the CVar in Malz chapter 8, a binomial inverses function is used to derive the no of defaults table 8.1. For the exam are we required to calculate these as well. If so please can u provide some insights on how to go about this? Sorry this maybe a simple question.

Hello @ijooma,

Please note that I moved your question here to a thread that discusses this. We would appreciate it, especially during this very busy time before the exam, if members would try to search for answers before posting a new thread. There are many threads in the forum that discuss Malz 8.1. Here are the two ways to find threads that may already answer your question. For this question specifically:

• Search (search the key words): https://forum.bionicturtle.com/search/?type=post
• Tag function:
  • https://forum.bionicturtle.com/tags/malz/
  • https://forum.bionicturtle.com/tags/malz-81/
  • https://forum.bionicturtle.com/tags/cvar/
  • https://forum.bionicturtle.com/tags/credit-var/

I hope this helps!

Nicole