Learning objectives: Calculate the theoretical price of a bond using spot rates. Derive forward interest rates from a set of spot rates. Derive the value of the cash flows from a forward rate agreement (FRA).
Questions:
713.1. Consider the steep spot (aka, zero) rate curve illustrated below: 3.0% at 0.5 years, 4.0% at 1.0 year, 4.6% at 1.5 years and 5.0% at 2.0 years. Each of these zero rates is per annum with continuous compounding.
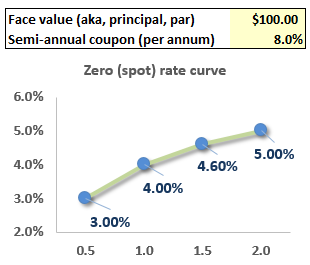
Which of the following is nearest to the theoretical price of a two-year $100.00 face value bond that pays an 8.0% semi-annual coupon (4.0% coupon every six months)?
a. $97.31
b. $99.47
c. $102.38
d. $105.62
713.2. Consider the steep spot (aka, zero) rate curve illustrated below: 2.0% at 0.5 years, 3.60% at 1.0 year, 4.40% at 1.5 years and 5.0% at 2.0 years. Each of these zero rates is per annum with annual compounding.
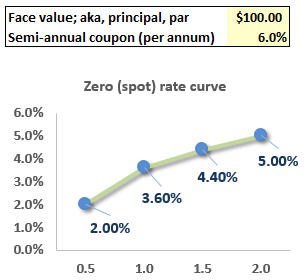
We are interested in the yield-to-maturity (aka, yield) of a two-year $100.00 face value bond that pays an 6.0% semi-annual coupon (3.0% coupon every six months). If this yield-to-maturity is expressed with semi-annual compounding (aka, bond equivalent basis), which of the following is nearest to this yield?
a. 2.52%
b. 3.95%
c. 4.88%
d. 5.00%
713.3. Consider the following steeply upward-sloping spot rate (aka, zero rate) curve where the per annum zero rates are given with continuous compounding (CC):

Which of the following is nearest to the implied six-month forward rate beginning in 1.5 years, F(1.5, 2.0), but where the six-month forward rate is expressed per annum with semi-annual compounding?
a. 3.78%
b. 4.80%
c. 5.90%
d. 6.50%
Answers here:
Questions:
713.1. Consider the steep spot (aka, zero) rate curve illustrated below: 3.0% at 0.5 years, 4.0% at 1.0 year, 4.6% at 1.5 years and 5.0% at 2.0 years. Each of these zero rates is per annum with continuous compounding.

Which of the following is nearest to the theoretical price of a two-year $100.00 face value bond that pays an 8.0% semi-annual coupon (4.0% coupon every six months)?
a. $97.31
b. $99.47
c. $102.38
d. $105.62
713.2. Consider the steep spot (aka, zero) rate curve illustrated below: 2.0% at 0.5 years, 3.60% at 1.0 year, 4.40% at 1.5 years and 5.0% at 2.0 years. Each of these zero rates is per annum with annual compounding.

We are interested in the yield-to-maturity (aka, yield) of a two-year $100.00 face value bond that pays an 6.0% semi-annual coupon (3.0% coupon every six months). If this yield-to-maturity is expressed with semi-annual compounding (aka, bond equivalent basis), which of the following is nearest to this yield?
a. 2.52%
b. 3.95%
c. 4.88%
d. 5.00%
713.3. Consider the following steeply upward-sloping spot rate (aka, zero rate) curve where the per annum zero rates are given with continuous compounding (CC):

Which of the following is nearest to the implied six-month forward rate beginning in 1.5 years, F(1.5, 2.0), but where the six-month forward rate is expressed per annum with semi-annual compounding?
a. 3.78%
b. 4.80%
c. 5.90%
d. 6.50%
Answers here:
