Learning objectives: Identify and describe the characteristics and pay-off structure of the following exotic options: gap, forward start, compound, chooser, barrier, binary, lookback, shout, Asian, exchange, rainbow, and basket
Questions:
731.1. Consider the price of an asset that begins and $30.00 and ends, after 20 periods, lower at $8.55. Also highlighted are its maximum ($39.23) and minimum price ($6.79) during this 20-period life:
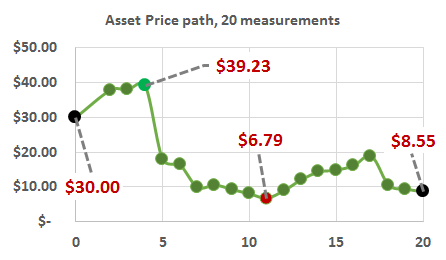
Among the following choices, which lookback option has the HIGHEST payoff if its life matches the 20-period interval shown?
a. Floating lookback call
b. Floating lookback put
c. Fixed lookback call with strike = $30.00 (matching the initial asset price)
d. Fixed lookback put with strike = $30.00 (matching the initial asset price)
731.2. Consider the price of an asset that begins and $30.00 and ends, after 20 periods, higher at $76.55. During this 20-period life, its maximum ($89.55) and minimum price ($23.58) are also highlighted:
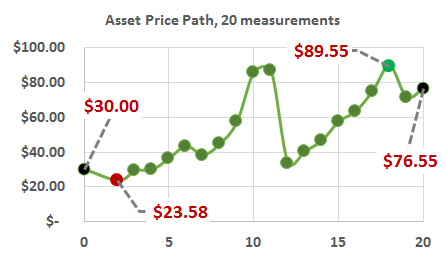
Among the following choices, which lookback option has the HIGHEST payoff if its life matches the 20-period interval shown?
a. Floating lookback call
b. Floating lookback put
c. Fixed lookback call with strike = $30.00 (matching the initial asset price)
d. Fixed lookback put with strike = $30.00 (matching the initial asset price)
731.3. Below is the output of a Black-Scholes (BSM) option pricing model for a one-year (T = 1.0) option with a strike price, K = $30.00, on a non-dividend-paying stock, q = 0%, when the stock price, S(0) = $30.00, with volatility, σ = 28.0%, while the risk-free rate is 3.0%. Under these assumptions, as shown, the price of a REGULAR European call option is $3.753 and the corresponding put option price is $2.866

However, assume that instead of a regular option, we are pricing Asian options under the same assumptions. In this case, there are four variations on the Asian option:
a. If N = 1, then the average price call and put are, respectively, $3.753 and $2.866
b. As we increase (N) from 1 to 252, the value of an average price call decreases from $3.753 to lower values
c. As we increase (N) from 1 to 252, the value of an average price put increases from $2.866 to higher values
d. As we increase (N) from 1 to 252, the value of an average strike put increases from zero to higher values
Answers here
Questions:
731.1. Consider the price of an asset that begins and $30.00 and ends, after 20 periods, lower at $8.55. Also highlighted are its maximum ($39.23) and minimum price ($6.79) during this 20-period life:

Among the following choices, which lookback option has the HIGHEST payoff if its life matches the 20-period interval shown?
a. Floating lookback call
b. Floating lookback put
c. Fixed lookback call with strike = $30.00 (matching the initial asset price)
d. Fixed lookback put with strike = $30.00 (matching the initial asset price)
731.2. Consider the price of an asset that begins and $30.00 and ends, after 20 periods, higher at $76.55. During this 20-period life, its maximum ($89.55) and minimum price ($23.58) are also highlighted:

Among the following choices, which lookback option has the HIGHEST payoff if its life matches the 20-period interval shown?
a. Floating lookback call
b. Floating lookback put
c. Fixed lookback call with strike = $30.00 (matching the initial asset price)
d. Fixed lookback put with strike = $30.00 (matching the initial asset price)
731.3. Below is the output of a Black-Scholes (BSM) option pricing model for a one-year (T = 1.0) option with a strike price, K = $30.00, on a non-dividend-paying stock, q = 0%, when the stock price, S(0) = $30.00, with volatility, σ = 28.0%, while the risk-free rate is 3.0%. Under these assumptions, as shown, the price of a REGULAR European call option is $3.753 and the corresponding put option price is $2.866

However, assume that instead of a regular option, we are pricing Asian options under the same assumptions. In this case, there are four variations on the Asian option:
- Average price call with strike, K = $30.00
- Average price put with strike, K = $30.00
- Average strike call (does not utilize a strike price)
- Average strike put (does not utilize a strike price)
a. If N = 1, then the average price call and put are, respectively, $3.753 and $2.866
b. As we increase (N) from 1 to 252, the value of an average price call decreases from $3.753 to lower values
c. As we increase (N) from 1 to 252, the value of an average price put increases from $2.866 to higher values
d. As we increase (N) from 1 to 252, the value of an average strike put increases from zero to higher values
Answers here
Last edited by a moderator:
