You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
par yield, YTM, and spot rate
- Thread starter ajsa
- Start date
Hi asja,
Not naive, the different yields are hard to sort through. I definitely discuss this in the tutorials in two places. This is why I made spreadsheet: http://www.bionicturtle.com/premium/spreadsheet/3.a.6_forward_rates/
(I recently added a second sheet precisely to illustrate the par yield)

In my example the spot rate curve = {1.5% @ 0.5 years, 2% @ 1.0 years...); i.e., an upward sloping zero rate curve
The zero rate curve is arguably the key market-based building block; i.e., the key input
The yield to maturity is not really a curve, it's a single number (it's implicity a flat curve, if you want to call it a curve).
The yield (YTM) "impounds" the zero rate curve information into a single number; e.g., if upward sloping zero curve, then the yield must be greater than the lowest zero and less than the highest.
The par yield is the coupon rate required to produce a bond price equal to par: it *does* also use the information in the zero rate curve, as it discounts each coupon by the appropriate zero (please try the second sheet, it is meant to illustrate the par yield)
so my shorthand summary would be:
spot (zero) curve: determined by the market. The input
yield to maturity: instrument-specific (i.e., varies by bond). Given that a given zero curve determines a price, the yield essentially "recasts" the zero into its equivalent flat yield curve; i.e., what unrealistic flat curve would give us the same bond price as we get from the realistic, actual non-flat curve?
par yield: given the spot curve, what coupon gives us price = par
Thanks, David
Not naive, the different yields are hard to sort through. I definitely discuss this in the tutorials in two places. This is why I made spreadsheet: http://www.bionicturtle.com/premium/spreadsheet/3.a.6_forward_rates/
(I recently added a second sheet precisely to illustrate the par yield)

In my example the spot rate curve = {1.5% @ 0.5 years, 2% @ 1.0 years...); i.e., an upward sloping zero rate curve
The zero rate curve is arguably the key market-based building block; i.e., the key input
The yield to maturity is not really a curve, it's a single number (it's implicity a flat curve, if you want to call it a curve).
The yield (YTM) "impounds" the zero rate curve information into a single number; e.g., if upward sloping zero curve, then the yield must be greater than the lowest zero and less than the highest.
The par yield is the coupon rate required to produce a bond price equal to par: it *does* also use the information in the zero rate curve, as it discounts each coupon by the appropriate zero (please try the second sheet, it is meant to illustrate the par yield)
so my shorthand summary would be:
spot (zero) curve: determined by the market. The input
yield to maturity: instrument-specific (i.e., varies by bond). Given that a given zero curve determines a price, the yield essentially "recasts" the zero into its equivalent flat yield curve; i.e., what unrealistic flat curve would give us the same bond price as we get from the realistic, actual non-flat curve?
par yield: given the spot curve, what coupon gives us price = par
Thanks, David
Last edited:
harifrm1980
New Member
Hi David,
Thanks for the great summary.
I noticed you used Excel's Rate function to calculate YTM to be 6.71% on the Par Yield tab. YTM appears to be the same as bond yield that hull calculates to be 6.76% on page 81. I checked discounting the coupon of $3 etc back to present and found that 6. 76% correctly discounts it back 98.39 but 6.71% does not. I am a little perplexed now, either Excel is doing it wrong or bond yield is not the same as the YTM.
Thanks.
Thanks for the great summary.
I noticed you used Excel's Rate function to calculate YTM to be 6.71% on the Par Yield tab. YTM appears to be the same as bond yield that hull calculates to be 6.76% on page 81. I checked discounting the coupon of $3 etc back to present and found that 6. 76% correctly discounts it back 98.39 but 6.71% does not. I am a little perplexed now, either Excel is doing it wrong or bond yield is not the same as the YTM.
Thanks.
Hi Hari,
Thanks for checking it, because you have revealed a mistake in my RATE() calculation:
1. I had RATE(5 periods,...) but for the 2-year bond it should be RATE (4, ..). Given that change, the correct entry in my Par Yield sheet should be a bond-equivalent yield (YTM) iof 6.88%
2. That bring us to the bond-equivalent yield of 6.88% versus your 6.76%. Both are valid: mine (following Tuckman) uses semi-annual compounding; discounting per a six month period and then multiplying the result by 2 (x2) to produce the bond-equivalent yield (which is less than the effective yield). Yours (following Hull) assumes continuous compounding/discounting.
... I hope the compounding difference explains the issue, and THANK YOU for finding an error in the formula (I am uploading a fresh XLS now)
David
Thanks for checking it, because you have revealed a mistake in my RATE() calculation:
1. I had RATE(5 periods,...) but for the 2-year bond it should be RATE (4, ..). Given that change, the correct entry in my Par Yield sheet should be a bond-equivalent yield (YTM) iof 6.88%
2. That bring us to the bond-equivalent yield of 6.88% versus your 6.76%. Both are valid: mine (following Tuckman) uses semi-annual compounding; discounting per a six month period and then multiplying the result by 2 (x2) to produce the bond-equivalent yield (which is less than the effective yield). Yours (following Hull) assumes continuous compounding/discounting.
... I hope the compounding difference explains the issue, and THANK YOU for finding an error in the formula (I am uploading a fresh XLS now)
David
In the text, we are told that spot rates > par rate for an upward sloping yield curve. However, this is confusing for me. Using the example in the book, if we are receiving 1.45% coupon payments and discounting using spot rates, we will end up with a price >100. My assumption is that to calibrate to par, we would need to discount using higher rates. However, the text states the opposite. Can anyone clarify?
Hi @bpdulog Here is a video I recorded that explains how the par yield is derived given (in this case an upward-sloping) spot/zero rate curve. To me, the hard part is the definition of par yield (the par yield is the yield-to-maturity that prices a bond exactly at par), so this is about the relationship between yield and the spot rate curve. In this video, the spot rate curve is upward sloping, such that the 4-year zero rate is 9.00% and the implied 4-year par yield is 8.57%. Here is the XLS used in the video @ http://trtl.bz/yt-par-yield
Hi @bpdulog Here is a video I recorded that explains how the par yield is derived given (in this case an upward-sloping) spot/zero rate curve. To me, the hard part is the definition of par yield (the par yield is the yield-to-maturity that prices a bond exactly at par), so this is about the relationship between yield and the spot rate curve. In this video, the spot rate curve is upward sloping, such that the 4-year zero rate is 9.00% and the implied 4-year par yield is 8.57%. Here is the XLS used in the video @ http://trtl.bz/yt-par-yield
Thanks @David Harper CFA FRM
I will watch at some point tonight. I think I realized a flaw in my comment. I think what the author is saying, and what may be in your video, is that the par rate is less than the spot rate for that particular maturity (e.g, the 4 year par rate < 4 year spot/zero rate) but can be greater than spot rates at lesser maturities (4 year par rate > 2 year spot rate). However, there is really no impact since the discounting is heavily anchored to maturity, when the principal is returned.
Hi @bpdulog Here is a video I recorded that explains how the par yield is derived given (in this case an upward-sloping) spot/zero rate curve. To me, the hard part is the definition of par yield (the par yield is the yield-to-maturity that prices a bond exactly at par), so this is about the relationship between yield and the spot rate curve. In this video, the spot rate curve is upward sloping, such that the 4-year zero rate is 9.00% and the implied 4-year par yield is 8.57%. Here is the XLS used in the video @ http://trtl.bz/yt-par-yield
Just watched it, excellent video!
trivzca
New Member
Hi David.. How Par yield is calculated in case of continuous rates?
Procedure is the same but the discount factors are calculated using:
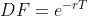
Then you just need to solve for the value of the coupon rate which brings the price = 100. You can do this very easily by setting up a spreadsheet to price the bond and then using the Excel solver to solve for the coupon rate.
Last edited:
Hi everyone,
When I think about yield curve I get really confused on how yield/rates are reported on the curve.
In this article for example:
https://blogs.cfainstitute.org/insi...tes-are-supposed-to-be-in-the-future-can-you/
The basic chart at the beginning of the article shows two yields for two different investments: a 2% yield on a 2 years investment and a 5% yield on a 5 years investment.
The confusion sits in the fact that, if a have to use this curve for discounting hypothetic cashflows at year 2 and at year 5 I will have to divide the cashflows respectively by (1+0.02)^2=1.0404 and by (1+0.05)^5=1.2763 (assuming discrete annual compounding)
My question is:
Shouldn't the yield shown on the curve be 4.04% at year 2 and 27.6% at year 5, rather than 2% at year 2 and 5% at year 5?
Thanks
When I think about yield curve I get really confused on how yield/rates are reported on the curve.
In this article for example:
https://blogs.cfainstitute.org/insi...tes-are-supposed-to-be-in-the-future-can-you/
The basic chart at the beginning of the article shows two yields for two different investments: a 2% yield on a 2 years investment and a 5% yield on a 5 years investment.
The confusion sits in the fact that, if a have to use this curve for discounting hypothetic cashflows at year 2 and at year 5 I will have to divide the cashflows respectively by (1+0.02)^2=1.0404 and by (1+0.05)^5=1.2763 (assuming discrete annual compounding)
My question is:
Shouldn't the yield shown on the curve be 4.04% at year 2 and 27.6% at year 5, rather than 2% at year 2 and 5% at year 5?
Thanks
Hi @filip313 that's interesting. To me the author's inaccuracy is to refer to the 2% and 5% as yields. Following Hull or Tuckman, we should call them spot rates or zero rates. It's true we see this {2% at 2 years, 5% at 5 years) called a yield curve, but it's really a spot rate curve. If the 2-year spot rate is 2.0%, then I agree with you that we discount a 2-year-forward cash flow--let's just say it is a $5.00 coupon to be received in 2.0 years--if the 2 year spot rate is 2.0% with annual compound frequency, to its present value with $5.0/(1+0.020)^2 = $4.806. It's similarly true that $1.00 today grows to $1.0 * (1 + 0.020)^2 = $1.0404 at the end of two years. Now, this is rarely discussed (and does not appear in the FRM) but the 1.0404 can be called a future value factor which is the "cousin" of the more familiar discount factor; the discount factor is the reciprocal of this future value factor because the discount factor (df) = $1.00/(1+0.020)^2 or (1+0.020)^-2 and it represents the present value of $1.00 received at the end of two years if discounted at 2.0% per annum with annual compounding.
There is an old saying that "discount factors don't lie" and it could be said of future value factors, too. The article assume, really, a spot (or zero) rate curve of 2.0% @ 2 years and 5.0% @ 5.0 years, and it is helpful to understand why these are stated or nominal spot rates, they are stated because they don't specify the compound frequency. But the 2-year discount factor of 0.9612 (and its cousin the 1.0404 future value factor) improve on the spot rates by incorporating the compound frequency. So this spot rate curve could also be represented by a discount function (i.e., set of discount factors): 0.9612 at 2 years and 0.7835 at 5 years. Getting to your point (maybe?), it would be atypical, but it could also be represented by a future value function: 1.0404 at 2 years and 1.2763. I hope that helps!
There is an old saying that "discount factors don't lie" and it could be said of future value factors, too. The article assume, really, a spot (or zero) rate curve of 2.0% @ 2 years and 5.0% @ 5.0 years, and it is helpful to understand why these are stated or nominal spot rates, they are stated because they don't specify the compound frequency. But the 2-year discount factor of 0.9612 (and its cousin the 1.0404 future value factor) improve on the spot rates by incorporating the compound frequency. So this spot rate curve could also be represented by a discount function (i.e., set of discount factors): 0.9612 at 2 years and 0.7835 at 5 years. Getting to your point (maybe?), it would be atypical, but it could also be represented by a future value function: 1.0404 at 2 years and 1.2763. I hope that helps!
The article's use of "yield" confused me as well. I agree with @David Harper CFA FRM's analysis but I think it's also important to remember that zero rate curves are derived from prices in the market. In order to do this you must be assuming a compounding frequency in order to derive the discount factors to price the instruments comprising the curve and back out the zero rates. This means that the curve you obtain ultimately has the compounding frequency "baked in" and that usage must be consistent.
For example, if you assume annual compounding when you derive the curve you will obtain slightly different zero rates than if you'd assumed continuous compounding. This means that when you use the curve to price another instrument you must assume annual compounding again otherwise the resulting price will not be consistent with the curve.
For example, if you assume annual compounding when you derive the curve you will obtain slightly different zero rates than if you'd assumed continuous compounding. This means that when you use the curve to price another instrument you must assume annual compounding again otherwise the resulting price will not be consistent with the curve.
Last edited:
@Matthew Graves Totally, agreed, thank you! fwiw, I only recently learned from Aleks (see https://forum.bionicturtle.com/threads/zero-rate-vs-spot-rate-vs-par-yield.6734/#post-22845) that "Spot rates are directly observable in the market. Zero rates are extracted from some asset to serve as a proxy for the spot rate. So, they are the same for pretty much all purposes, but there is that distinction."
Hi @filip313 that's interesting. To me the author's inaccuracy is to refer to the 2% and 5% as yields. Following Hull or Tuckman, we should call them spot rates or zero rates. It's true we see this {2% at 2 years, 5% at 5 years) called a yield curve, but it's really a spot rate curve. If the 2-year spot rate is 2.0%, then I agree with you that we discount a 2-year-forward cash flow--let's just say it is a $5.00 coupon to be received in 2.0 years--if the 2 year spot rate is 2.0% with annual compound frequency, to its present value with $5.0/(1+0.020)^2 = $4.806. It's similarly true that $1.00 today grows to $1.0 * (1 + 0.020)^2 = $1.0404 at the end of two years. Now, this is rarely discussed (and does not appear in the FRM) but the 1.0404 can be called a future value factor which is the "cousin" of the more familiar discount factor; the discount factor is the reciprocal of this future value factor because the discount factor (df) = $1.00/(1+0.020)^2 or (1+0.020)^-2 and it represents the present value of $1.00 received at the end of two years if discounted at 2.0% per annum with annual compounding.
There is an old saying that "discount factors don't lie" and it could be said of future value factors, too. The article assume, really, a spot (or zero) rate curve of 2.0% @ 2 years and 5.0% @ 5.0 years, and it is helpful to understand why these are stated or nominal spot rates, they are stated because they don't specify the compound frequency. But the 2-year discount factor of 0.9612 (and its cousin the 1.0404 future value factor) improve on the spot rates by incorporating the compound frequency. So this spot rate curve could also be represented by a discount function (i.e., set of discount factors): 0.9612 at 2 years and 0.7835 at 5 years. Getting to your point (maybe?), it would be atypical, but it could also be represented by a future value function: 1.0404 at 2 years and 1.2763. I hope that helps!
Thank you David.
That's exactly what I mean. Without an explicit indication of the compound frequency and of the type of yield , the generic concept of yield/yield curve is not precise.
Hi David,Hi asja,
Not naive, the different yields are hard to sort through. I definitely discuss this in the tutorials in two places. This is why I made spreadsheet: http://www.bionicturtle.com/premium/spreadsheet/3.a.6_forward_rates/
(I recently added a second sheet precisely to illustrate the par yield)

Thanks, David
Surprisingly, I am not able to access the link?

Hi @lalit74 sorry but that's a really old post of mine, I am surprised that I did find the XLS, here it is https://www.dropbox.com/s/wcj2ls7uh6efawm/0721_par_yield.xls?dl=0
Similar threads
- Replies
- 2
- Views
- 454
- Replies
- 6
- Views
- 609
- Replies
- 2
- Views
- 1K
- Replies
- 3
- Views
- 1K
